Mesh analysis is a method that is used to solve planar
circuits for the currents at any place in the circuit.
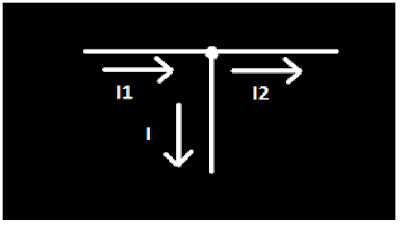
Find I
In solving mesh current you can decide whether you go
counter-clockwise or clockwise in applying KCL or creating a loop but I always
use the direction of the given current to avoid sign errors.
I1 is already given in the circuit which is 2 A. The
only current that we need to solve is I2 to identify current I.
From I2 we
could get the equation:
-5 (I2 –I1) + j3 (I2) – 5 =
0
Transpose 5 and substitute I1 to the equation.
-5 I2 + 5 (2) + j3 I2= 5
-5 I2 + 10 + j3 I2= 5
(-5+ j3) I2= 5- 10
(-5 + j3) I2 = -5
I2= -5/ -5+ j3
I2= 0.735+ j0.441
To get current I we could
use this illustration taken from the middle top node.
(The current entering the
node is equal to the current leaving the node.)
Therefore:
I1= I + I2
I= I1- I2
I= 2- (0.735+ j0.441)
I= 1.2647-
j0.441
Convert it to Polar.
I= 1.339 ∟-19.22 A
Supermesh
A super mesh is created when there are two meshes that
have a current source in common. When a super mesh occurs in a circuit it
involves opening the given current and combining the formulated equation of the
two loops that are connected to the given current. Then applying KCL to the
original circuit to get another equation and applying matrix, ohms law or
simple calculations to obtain the unknown value in the circuit.